
If you don't like this rule, here are a few other mnemonics for you to remember:
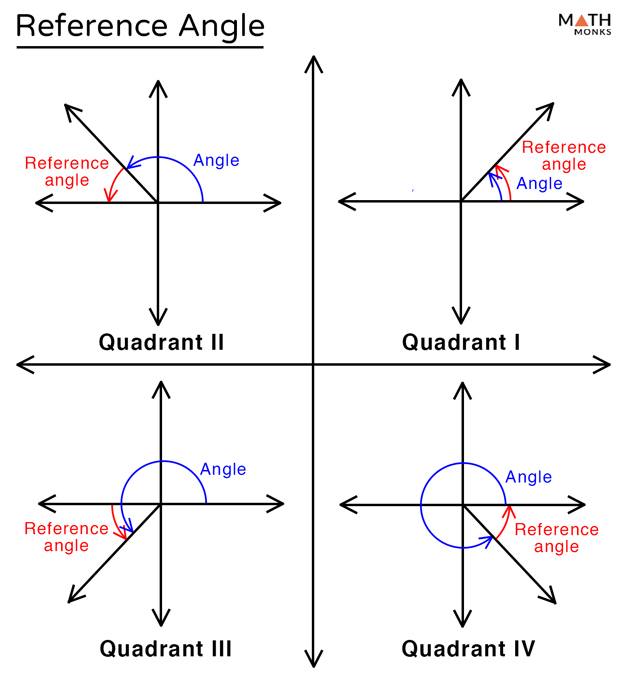
C for cosine: in the fourth quadrant, only the cosine function has positive values. T for tangent: in the third quadrant, tangent and cotangent have positive values. A reference angle always uses an x-axis as its frame of reference. Their value is always between 0 and 90° when measured in degrees or 0 and /2 when measured in radians. S for sine: in the second quadrant, only the sine function has positive values. Reference Angle The reference angle is used for simplifying the calculations related to trigonometric functions with different angles. A for all: in the first quadrant, all trigonometric functions have positive values. Follow the "All Students Take Calculus" mnemonic rule (ASTC) to remember when these functions are positive. The only thing that changes is the sign - these functions are positive and negative in various quadrants. Generally, trigonometric functions (sine, cosine, tangent, cotangent) give the same value for both an angle and its reference angle. Numbering starts from the upper right quadrant, where both coordinates are positive, and goes in an anti-clockwise direction, as in the picture. This is done using corresponding reference angle in the first quarter as discussed above in the ‘Reference Angles and Trigonometric Functions’ section.The two axes of a 2D Cartesian system divide the plane into four infinite regions called quadrants. Assume that the original angle is Quadrantġ) Used to find the value of an angle with trigonometric functions such as the sine or cosine value of any angle. Given below is a table showing the values of reference angles in radians and degrees in the four coordinate planes. When calculated in radians: 180° = π, 360° = 2π, 270 = 2π/2, and 90° = π/2Ĭase 1: (For Angles between 0° to 90°) – First quadrantĬase 2: (For Angles between 90° to 180°) – Second quadrantĬase 3: (For Angles between 180° to 270°) – Third quadrantĬase 4: (For Angles between 270° to 360°) – Fourth quadrant So, if the given angle is 310°, then its reference angle is (360° – 310° = 50°). So, if the given angle is 200°, then its reference angle is (200° – 180° = 20°).Ĭase 4: (For Angles between 270° to 360°) – When the terminal side is on the fourth quadrant, the reference angle is 360° minus our given angle. So, if the given angle is 105°, then its reference angle is (180° – 105° = 75°).Ĭase 3: (For Angles between 180° to 270°) – When the terminal side is on the third quadrant, the reference angle is the given angle minus 180°. So, if the given angle is 45°, then its reference angle is also 45°.Ĭase 2: (For Angles between 90° to 180°) – When the terminal side is on the second quadrant, the reference angle is 180° minus our given angle. There are four possible cases:Ĭase 1: (For Angles between 0° to 90°) – When the terminal side is on the first quadrant, the reference angle is the same as the given angle. We can find reference angles depending on which quadrant the terminal side of the angle is located in either degrees or radians. #Reference angle how to#
‘C’ for cosine: In the fourth quadrant, only the cosine function has positive value Formulas How to Find a Reference Angle ‘T’ for tangent: In the third quadrant, tangent and cotangent have positive values ‘S’ for sine: In the second quadrant, only the sine function has positive value
‘A’ for all: In the first quadrant, all functions have positive value

The only thing that varies is the sign.įollow the mnemonic rule: ‘ Add Sugar To Coffee’ or ‘ All Students Take Calculus’ to remember when these functions have positive values. Normally, the four trigonometric functions: sine, cosine, tangent, and cotangent give the same value for an angle and its reference angle. The numbering starts from the upper right one, the first quadrant, where both coordinates are positive as we continue to move in the anticlockwise direction. The two axes, x, and y divide the plane into four quadrants, named I, II, III, and IV. Reference Angles and Trigonometric Functions Looking at the picture above, every angle is measured from the positive part of the x-axis to its terminal side by traveling in a counterclockwise direction. Their value is always between 0 and 90° when measured in degrees or 0 and π/2 when measured in radians. The reference angle is used for simplifying the calculations related to trigonometric functions with different angles.







 0 kommentar(er)
0 kommentar(er)
